Constructing binary trees using relative branch encoding
In this third article in what is rapidly becoming a series on binary trees, we’ll have a look at another way of constructing generic binary trees from a serialised format. For this, we’ll build on some of the techniques and insights from the previous articles:
- Reconstructing binary trees from traversals: the initial post which dealt with constructing binary trees from pre-order and in-order sequences
- Creating a forest from a single seed followed up by creating different trees conforming to the same pre-order sequence.
In the first article we covered how a generic (unordered) binary tree cannot be constructed from a single depth-first search sequentialisation. Lacking structural information, a second sequentialisation is required, in-order with one or pre or post-order. This is all well and good when the values in the tree are small (measured in bytes), but as they get larger, there is a considerable overhead in this duplication of values. Compression will certainly help, but is unlikely to remove it entirely.
The second article introduced the notion of attachment loci of a tree under construction: the possible locations where the next node/value from a pre-order sequence could be placed. We only needed them for constructing tree permutations at the time, but with a few tweaks, we should be able to use them to provide the structural information to supplement the single sequentialisation.
Structured depth-first search
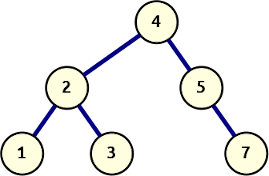
Let’s start with that last idea. We take the basic recursive depth-first search algorithm and extend the return value to include the attachment point of the node value returned. We’ll assign the furthest-right locus 0 and number up from there. This means adding a 1 for every time we recurse and explore a left branch.
The generator below yields tuples with an absolute branch location and the value at that location, in pre-order sequence:
def dfs_structural(node: Node, branch_id: int = 0) -> Iterator[Tuple[int, Any]]:
if node is not None:
yield branch_id, node.value
yield from dfs_structural(node.left, branch_id=branch_id + 1)
yield from dfs_structural(node.right, branch_id=branch_id)